|
Thanks to a recent Twitter post by Brette Garner at the University of Denver, I came across an interesting article by the NCTM (National Council of Teachers of Mathematics) published in The Mathematics Teacher. The journal title is “Effect of Certain Types of Speed Drills in Arithmetic” by A.I. Messick. The study split 272 fourth and fifth graders into two groups while teaching addition: one focused on speed and the other focused on accuracy. Here are a few of the conclusions: (1) Accuracy is more important than speed, (2) From the viewpoint of speed, it makes little difference which is emphasized, speed or accuracy, (3) From the viewpoint of accuracy, it is much better to emphasize accuracy, and (4) In teaching addition to pupils of the fourth and fifth grades of the elementary schools it is better to emphasize accuracy rather than speed. Given recent work by Professor Jo Boaler and her group at Stanford and the NCTM’s definition of math fluency as being accurate, flexible, and efficient with computations, research concluding that teaching accuracy over speed does not come as a surprise. What I did find surprising; however, is that this article was published in 1926. Not 1996, not 2006 or even 2016, but 1926. Since 1926, how many thousands of students have suffered through timed math often known as “mad minutes” that focus on speed? How many students were discouraged from studying engineering, science, medicine, or other disciplines because they thought that being good at math meant memorizing procedures and regurgitating facts quickly? How many scientists did we fail to create since 1926 because memorizing mathematical procedures was a gatekeeper to further study of all sciences? But, wait. 8 x 7 is always 56, right? You just have to know that quickly. If you can’t recall this immediately, then how can you possibly go on to study fractions or solve differential equations? I would argue that knowing how to figure out 8 x 7 flexibly, accurately, and efficiently is much more meaningful than rapid recall or memorization. When I was a high school teacher, I found too many students who could not answer questions like, “What is 8 x 7?” When students are taught their times tables through “mad minutes” or other techniques that rely on speed, they might remember them in the short term, but will not be able to recall them years later. In particular, many high schoolers struggled to recall the 8 times tables. When I would ask them the answer to 8 x 7 they would blurt out 52, 58, or some other incorrect answer. When I said, ”no,” they usually would look at me with a puzzled look, shrug their shoulders and say, “Hmmmm...I don’t know,” or reach for their calculator. Instead of giving up or relying on technology for simple facts, I want to live in a society of people who, when they forget a simple fact like 8 x 7, have another way to figure it out efficiently. One possible scenario: I can’t recall 8 x 7, but I know that 10 x 7 is 70 and I need to take away 2 x 7 which is 14, leaving me with 56. So, 8 x 7 is 56. There are multiple other ways to answer this question without using pencil & paper or relying on a calculator. This is true mental math because it relies on problem-solving and making connections between various numbers and operations. Regrettably, many people equate mental math to “mad minutes” and rapid regurgitation of facts. A student who understands multiple ways to calculate 8 x 7 exhibits true number sense. If we rely solely on rote procedures and memorization, we produce students and adults who only have one way to approach a question like 8 x 7. When their memory fails, they are at a loss at what to do to find the answer. Making Math Moments that Matter, a podcast and wonderful website curated by Kyle Pearce & John Orr, recently Tweeted that “teaching math exclusively from your textbook is like teaching with a bag over your head.” That statement really resonates with me because when teachers teach solely from a text, they are teaching a very one dimensional view of mathematics. What other types of activities might students engage with to learn the content? What questions might they come with on their own if they are given fewer prompts & procedures to mimic? What technology currently exists that might not have been available when the textbook was published? Given what we know about current best practices in math, how can teachers lift the paper bags off of their heads? To explore these ideas, I reflect back upon my journey as a high school math teacher. When I first started teaching, I was very much a follower of the textbook and had that paper bag firmly planted over my head. In fact, I remember the first few weeks at my first international school in Caracas in 1999. The book order was delayed and had not been delivered. How could I teach IB math without a textbook? The mere thought paralyzed me. I thought I was a good teacher because I was good at explaining procedures found in the textbooks to my students. If I made my explanations clear in their delivery, then I was doing my job. I had missed the whole point by focusing on what I was doing rather than on what students are learning. As a mathematics consultant, I now support teachers today in discovering how math can be learned through applications and problem solving. As a new teacher, I only gave problem-solving lip service. My early students solved the word problems found at the end of the chapter and did very little true problem solving. What changed in my thinking and in my practice? How did I remove the paper bag from my head? I had to learn to let go by starting small and trusting that my students would still learn the necessary content. This was not easy for me to do and it can be very scary. I loved being the sage on the stage. I was comfortable there and received positive feedback from students who told me they enjoyed my math classes. Looking back on my early days as a teacher, I wasn't teaching much mathematics. I was teaching tricks, procedures, and “how to’s.” I was an expert at helping students make sense of textbook problems, which meant explaining procedures and tricks to them clearly. What I wasn’t doing was creating experiences for my students to be true problem-solvers. How can we provide all students the opportunity to problem-solve and make meaning of the mathematics they are learning? How can teachers shift their math instruction? I offer three suggestions:
Starting small is often one of the most difficult things for educators to wrap our heads around. If there is a better way of doing things, then I need to throw out the textbook tomorrow, find all my own resources based on the standards, and spend five hours preparing for every lesson. No. Instead, take one thing from one lesson and change it. Consider one learning outcome from a lesson and find an interesting problem (lots of places to start here) that involves more student thinking and less teacher direction. If you’ve never done this before, it can be very hard to let go. Note: you don’t have to make up your own problems at the start, you can try an open middle or youcubed problem. Here is an example from Jo Boaler: Both questions explore the concept of area. But the second allows for student exploration, creativity, and conversations about what area means.
Secondly, join a PLN with other educators who are also interested in teaching math differently. They might be at your school or across the globe. It might be through a Critical Friends Group or through work with an instructional coach. There is nothing better than being able to share a success, no matter how small, with supportive colleagues. Twitter is a great place to start. I learn so much on Twitter from the math and education people whom I follow. There is a plethora of information out there and you can be selective over what pops up on your feed. You might find a fellow teacher who lives in a different country, but with whom you connect and share great ideas. There are Facebook groups devoted to teaching math. Don't be afraid to put yourself out there virtually or in person. Finally, inform your students about what you are doing. If they have been taught traditionally for years, they are used to sitting and getting the information from the sage on the stage. This type of passive learning is much easier than having to engage in problem solving. If they don’t understand why you are doing things differently and prepare them for it, there might be unnecessary pushback. Sometimes, when using a “student-as-worker, teacher-as-coach” approach to instruction, students assume you don’t know the answers. If you tell them at the start that you do in fact know the answers, I find they are more willing to dig into the problems. I used to tell my students, “Yes, I know the answers to the questions you are working on. No, I’m not going to tell you even though I know.” I also shared this information during parents’ night. I had very little parent pushback because I invited them into the conversation and gave them the resources to support their children outside of the classroom. If their child’s math class looks different, it’s our job as educators to help parents navigate this. If not, it can lead to viral misinformation, like the father who wrote a check using Common Core math. My journey from teacher of procedures, to teacher of mathematics, to mathematics consultant has not been linear. In fact, it has been anything but that. I am continually growing and learning as I continue along this path. I enjoy supporting teachers as they find their own paths to teaching more of the beauty of mathematics and fewer procedures. I became a math consultant because I am passionate about empowering educators with the mathematical expertise needed to inspire the problem solvers of the future. I love sharing my triumphs and failures in a vulnerable way to help both beginning and experienced teachers grow. Is there one thing you’d like to do differently in your math classroom? Try it today. Take that first step and let me know how it goes.
0 Comments
When I taught high school mathematics, my first homework assignment was always a math autobiography. I asked students to tell me about themselves through the lens of mathematics. I offered them a few prompts, but purposely left the assignment general so they could interpret it as they saw fit. Writing wasn’t required. I told them if they best expressed themselves through a mathematical interpretive dance then go for it! Unfortunately, no one ever took me up on that offer. However, I did have more than one high schooler adorn their papers with stickers, drawings, write a poem, or create other personal representations of their mathematical journeys. What was the most common phrase from their autobiographies? I used to like math until… I used to like math until my 7th grade teacher made me solve problems at the board in front of the class. I used to like math until my teacher handed back our math tests in order - highest grade to lowest. I used to like math until my 4th grade teacher told me girls don’t do well in math (this came from a grade 10 student in 1999). I used to like math until middle school and then it made no sense to me. I read my students’ mathematics autobiographies only after I had learned all of their names. Not only was it a way to get to know the group of learners in front of me, but it gave me insight into some of the math baggage most students carried, and they carried a lot of baggage. What are we doing as a math community to stop the phrase I used to like math until? Whenever I visit Twitter, I feel like we are doing a lot. Twitter is alive with practical examples of empowering students to become problem solvers instead of followers of rote procedures. I would be shocked and saddened to hear that an elementary teacher told a girl that she can’t do as well in math as the boys. There is an entire program, MidSchoolMath, focused around the middle school math cliff, acknowledging that something happens in middle school to our math learners. However, this is not an issue that occurs only in middle school. How many high school teachers hear the question, “When are we ever going to use this?” If the only response is for the test or for next year’s class, how can we expect students to be motivated to learn the topic that is in front of them that day? If we can’t come up with a real example of an application of the mathematics, then why are we teaching it? Better yet, what questions are we asking our students or what agency do they have to make their own connections to the world around them? And please don’t tell me we have to teach a topic because it’s in the standards. When James Tanton, a mathematician-at-large for the Mathematical Association of America, taught high school mathematics, he realized that he had to teach polynomial division to his high school students. I love his response. "My charge: Teach polynomial division to high-schoolers. My reaction: Why?" -- Dr. James Tanton (quote taken from Math Recess by Sunil Singh & Dr. Chris Brownell) He thought outside of the box and created Exploding Dots, which has now grown to be an international movement though the Global Math Project. It is possible to do things differently, even when a topic is “in the standards.” And, if you don’t know about exploding dots, now is the time to explore them. Don’t wait! One of my goals as a high school teacher was to change the attitudes of students who told me at the start of the year in their autobiographies that they didn't like math or weren’t any good at math. Which, unfortunately, was often a majority of the class. Did I always succeed? No. But I hope that I was able to give even the most reluctant learners a glimpse into how math could be enjoyable and not something to fear. These were the days before Twitter and Jo Boaler entered my life with her empowering research on the importance of a math mindset. So, I did my best with the resources I had. How can we ensure that all of our learners know they have a place in our mathematics classrooms? How do we prevent one more student from ever saying, I used to like math until? It isn’t easy, but it is crucial if our goal is to nurture students who are excited to take MORE math classes in high school for the right reasons. That is, not just for their college applications, but because they find joy in exploring the beauty of mathematics and wonder what discoveries are yet to be found. What empowering experiences will your math students explore today? Here are a few places to find some inspiration. For the past five years, I've called Saudi Arabia my home. Before that, home was China and prior to that, it was India. My summer home in the U.S. is in beautiful, Ithaca, New York. As an international educator and now international educational consultant, I couldn't imagine home looking any other way. I grew up in Orefield, Pennsylvania. Unlike my own children, I attended the same school district from grades K-12. I didn't get on an airplane until I was 18 years old. I return to Orefield once a year to visit my father, who still lives in the same house where I grew up. I also catch up with "old" friends. This past summer, I was fortunate enough to meet up for coffee with one of those friends who teaches middle school math. In fact, she teaches at the same school where she and I first became friends over thirty years ago! Our friendship is deep and has weathered the course of time and distance. Relationships like this are special and unique. We talked about my new consulting business and she shared how she was looking for ways to reinvigorate her math teaching after 24 years in the classroom. I shared a few of my favorite resources and articles and pointed her in the right direction of a few more. We texted a few times at the start of the school year as she delved into the resources I shared. In early October, she posted this on her Facebook page: Yesterday I gave one of my classes this prompt and nothing else. No directions, no instructions, no rules. I handed out the prompt, told them they could form groups and see what they could come up with. Before I even finished handing out the papers, I got a "Is this graded?" At first there was frustration and confusion. Students were stunned. "What are we supposed to do?" It didn't take long for some to start to make observations, to ask questions and to "solve" the problem. One group was shocked when they came to me to share that they solved it and I told them to keep going. Keep going? Isn't there only one right answer? Are we right or wrong? Today we started by sharing our questions, observations and "answers" to the prompt. Then the magic really began. Groups started exploring patterns. Students tested their theories, changed the "rules" and tested some more. The bell rang and we all left wanting more. The energy, conversations and excitement was incredible. Many students told me I should start a club like this because they enjoyed it so much. Some may say I "lost" two days of instruction with my Algebra I class and anyone in education knows how important those days are with looming Keystone Exam dates. I personally consider these past two days priceless. Thank you to an incredible math instructor, coach and friend for helping me to re-energize my math self. Thank you, Nicole Fedio. These are the moments in coaching relationships that matter. What made this relationship particularly easy is that my friend and I had decades of history together where we could be vulnerable with one another. The number one priority when I am working with a teacher is our relationship. If our coach-teacher relationship is not a mutual one of respect and openness, then as a coach, I am "dead in the water."
What I find most interesting about my conversation and subsequent texts with my friend is that from my perspective, I don't feel like I did much, other than encouraging her and pointing her in the right direction. SHE is the one who decided to take a risk with her students. SHE is the one who watched videos, read the articles, and follow the links I shared. SHE is the one doing the heavy lifting. I am simply a guide on side, simultaneously learning from her. Magic happens when coaches and teachers are able to find that "sweet spot" of working together. How can these relationships be cultivated and maintained when there isn't 30 years of history between the coach and teacher? I my opinion, it's vulnerability, openness, and a true passion for learning. Thank you, Melissa, for sharing your awesome work with me.  Image from: http://www.cambridgeblog.org/2019/08/information-overload-in-the-legal-sphere/ Image from: http://www.cambridgeblog.org/2019/08/information-overload-in-the-legal-sphere/ Bar Models, open middle, three-act math tasks, esti-mysteries, numberless word problems, rich tasks, number talks, unit chats, which one doesn’t belong’, choral counting, Desmos, GeoGebra, Youcubed… What have I missed? This list goes on and on. I know there are other great resources out there that I could have mentioned. Does this list start to make you feel a little like the picture above? Some days it does to me. The educators who have created these mathematics resources are an amazing group of people who I follow on Twitter. I am continually awed by their ability to create meaningful material that inspires teachers around the globe. What’s especially wonderful about these resources is that they are all free and readily available to teachers with a quick Google search. What's not so wonderful is that there really isn't such a thing as a "quick Google search" when it comes to lesson planning. If some of these names are new to you (What in the world is choral counting?) it can be very daunting to try them out with your students. It’s very easy to suffer from information overload, especially in the world of Twitter and other social media. Information overload can cause us to be paralyzed. AAHHHH… there’s just too much out there…. it’s easier for me to just keep doing what I’ve always done. Where can I even start? If you feel this way, you are not alone. Where to begin? Start small. Are your students struggling to learn multiplication facts? Look at youcubed for some resources. Try a multiplication number talk. Pick one new resource to try, and stick with it. And give yourself grace, the implementation dip is real. Ask your colleagues or coach for feedback. If you are fortunate enough to work at a school with a learning coach, invite them into your classroom. If you don’t have a coach, try something like an observe me protocol to invite feedback from colleagues. Let go. This is one of the most challenging things about trying new things as an educator. Experience is both a blessing and a curse. If I’ve successfully taught a topic the same way for many years, why should I try to teach it a new way? My answer to that is Why not? What is holding you back? Two high school teachers I worked with last year were amazed at the quality of projects their 9th grade students independently created using Desmos. What did the teachers do differently? They let go of their thinking that they needed to teach the material the way the textbook did. The students met the same learning objective, but in a different way. Sifting through the sheer number of math resources out there takes a lot of time. Time is a limited resource for most educators. Want to try something new but don’t know where to begin? Reach out to me via email or the comments section to get started. links to these resources can be found here: Bar Models, open middle, three-act math tasks, esti-mysteries, numberless word problems, rich tasks, number talks, unit chats, ‘Which One Doesn’t Belong’, choral counting, Desmos, GeoGebra, Youcubed The longer that I am in education - the more books I read, conferences I attend, workshops I give, Twitter feeds I follow - the more I realize just how much I have to learn. Because of the very nature of our craft, teaching is a reflective process. Even when I taught a killer lesson and thought to myself “nailed it” there was always that nagging voice in my head saying, ”But you could have done this instead…”
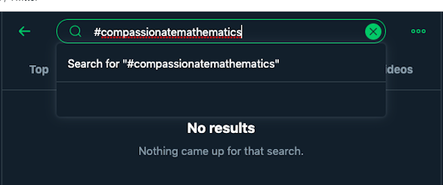
The more I learn, the more I explore what it means to be a ‘good teacher’, the more I reflect back on my time as a high school teacher and want to cringe. I sincerely need to apologize to many of my former students for all the times I made the wrong decision, said the absolute wrong thing, and even taught the mathematics incorrectly (2001-2002 Nathan Hale AP Calculus students, I’m looking at you!) These are the moments that still haunt me now, many years later. I can name too many times when I did not show compassion towards my high school students and their complex lives outside of school. Math class had to come first! I regularly assigned a compassion-less amount of homework. Not to mention all of the students that I taught in a very procedural way during my first few years in the classroom. I perfected the "sage on the stage" approach to teaching. Reflecting back now, I didn't know what I didn’t know. Do you know who did know that there was a more effective way to teach mathematics? The NCTM. In 1980, it published An Agenda for Action and in 1989, Curriculum and Evaluation Standards for School Mathematics. The NCTM has been calling for reform in mathematics education since I was a student. Principles to Actions arrived in 2014. In 1994, Steve Leinwand wrote Four Teacher-Friendly Postulates for Thriving in a Sea of Change. These postulates are still relevant and timely to math teachers today. I chuckle whenever I hear the phrase “new math.” Educators like Steve Leinwand and organizations like the NCTM have been calling for change for decades. This is not new. What is new is that teachers and schools are finally listening and change is occurring. If you are a former student of mine, please know that I continue to grow from my mistakes. If you are a teacher who is bravely trying something new this year, sometimes that is enough. I recently read an excellent article by Sunil Singh, Mathematics: In the Age of Brene Brown, about failure and vulnerability in the mathematics classroom. As teachers, not only do we need to show vulnerability, but we need to practice self-compassion when we are vulnerable. Instead of looking backward and only saying what I could have done differently, I acknowledge and own my past mistakes and use them to inform my future. My mission is to use my past experiences, mistakes and all, to help other educators learn and grow and they undertake the very complex and wonderful job of teaching mathematics. I recently conducted a Twitter search that surprised me. I was expecting to find a few more results for #compassionatemathematics. Is the lack of results because many adults associate mathematics with negative feelings and the word compassion is the farthest thing from their minds when they hear the word math? Math trauma is definitely a 'thing.' Is it because compassion is often associated with with humanities and not sciences?
Oxford defines compassionate as "feeling or showing concern for others." When I reflect on my time as a student, I don't think I always showed much concern for others. In 3rd grade, I was the first student in my class to memorize all the times tables. When we started studying multiplication, we had a daily quiz starting with the 1 times tables, working up to the 12s. Each student had a paper ice cream cone on the class bulletin board. If you scored perfect on the daily quiz, you placed a paper scoop of ice cream on your cone. The first student with 12 scoops won a Coke. Did I care about the other students who took longer to reach that goal? Nope. Give me my Coke. I won that Coke. And I definitely felt like I was smarter than others because I won the race to the top of my ice cream cone. The system of math education that ensued rewarded memorizers like me while leaving others feeling like they didn't have the 'math gene.' I wouldn't define it as very compassionate. Interestingly enough, Oxford defines compassion as “sympathetic pity and concern for the sufferings or misfortunes of others." Oh my. Maybe compassionate mathematics isn’t a ‘thing’ because too many math learners are busy pitying themselves as they suffer through textbook pages of problems that can be solved by procedures or memorized algorithms. How can they feel compassion for others when they themselves are mired down with rote math learning? Or maybe students are too busy working through textbook practice pages of similar problems instead of communicating and exploring with one another. When I hear “compassionate mathematics” perhaps I am thinking about how mathematics can be taught in a more humane way? This has been on my radar lately because of a recent Virtual Conference on Humanizing Mathematics that I've been following. But humanizing math and showing compassion are not the same thing. I dislike the word 'pity' but the word concern resonates with me. How can we help students show more concern for others during math class? One way is to provide them with learning opportunities that connect them with other students in meaningful ways. Jo Boaler is leading the charge with this. Her resources on youcubed provide examples that encourage students to make sense of mathematics while recognizing that often there is more than one way to approach a problem. I can't help but wonder what connections I might have made as a third grader if I had been given the opportunity to explore something like the Four 4's problem with my classmates instead of racing against them to recall my 8 times tables. What can we do as teachers to be more compassionate towards our math learners? We can be concerned when a student is having an “off day” and can’t seem to get their head in the game of math. Instead of carrying on through a lesson that few students are understanding, we can pay attention to our students and their visual cues that they 'aren’t getting it.' We can find ways to make the math meaningful and relevant to them. We can make changes if a student does feels like he or she does not have a place in our math classroom. Again, Jo Boaler reminds us that there is no math gene and all students can learn math to the highest level. As a high school teacher, at times I prioritized math and the race to cover the syllabus over the needs of the humans I was teaching. I regret that now as I definitely was not showing much compassion. Ultimately, compassionate math is much more than going to youcubed and downloading some mindset posters to put on your walls. It's a mindset that needs to be explored, pondered, and cultivated with like-minded educators. I think there’s also an important self-compassion piece to it. More on that later. P.S. I hold no ill-will or judgement towards my third grade teacher. She was a wonderful teacher and I know that she was doing exactly what most teachers did in a 1981 math class. I wonder what learning environment she might have created with youcubed as one of her resources? |
Nicole FedioMathematics Consultant at Mathematique Archives
February 2020
Categories |


 RSS Feed
RSS Feed
